Improving Cursor Tab with online RL
At Cursor, our goal is to make developers an order of magnitude more productive. An important part of that goal is Cursor Tab, our system that predicts your next action across your codebase. Whenever you type a character or move your cursor within the editor, our Tab model tries to predict what you’ll do next, and if it has sufficient confidence, we’ll display its prediction as a suggestion that you can accept by pressing Tab.
Our Tab model runs on every user action, handling over 400 million requests per day. As a result, we have a lot of data about which suggestions users accept and reject. This post describes how we use this data to improve Tab using online reinforcement learning.
Our approach is unusual because it involves rolling out new models to users frequently throughout the day and using that data for training. Most other LLM providers train on static datasets or use paid labelers, and only roll out a new model to users as part of a named model release every few months.
The problem of noisy suggestions
We try to keep the accept rate of Tab suggestions high. If the accept rate is low, it means we’re showing too many incorrect suggestions, which is distracting and disrupts the flow of coding.
Achieving a high accept rate isn’t just about making the model smarter, but also knowing when to suggest and when not to. Sometimes there simply isn’t enough information to know what action the user is going to take: even if the model had perfect knowledge and reasoning ability, it wouldn’t know what the user will do. In these situations, we shouldn’t suggest anything.
To increase the accept rate of the model’s suggestions, one simple approach is to train a separate model to predict whether the suggestion will be accepted. In 2022, Parth Thakkar found that GitHub Copilot used this approach, deriving a “contextual filter score” using a logistic regression model taking 11 features as inputs, including the programming language, whether the previous suggestion was accepted or rejected, the trailing characters before the user’s cursor, and other features. It’s unknown what signal this model was trained to predict, but our best guess is that it’s predicting the likelihood that the user will accept a suggestion if one is shown. When the score is lower than 15%, the suggestion is skipped and nothing is shown.
This solution is viable, but we wanted a more general mechanism that reused the powerful representation of the code learned by the Tab model. Instead of filtering out bad suggestions, we wanted to alter the Tab model to avoid producing bad suggestions in the first place. Therefore, we opted to use policy gradient methods instead.
The policy gradient
Policy gradient methods are a general way to optimize a “policy” (in this case, the Tab model) to increase a “reward”. The reward is a number that we assign to every action taken by the policy. By using a policy gradient algorithm, we can update the policy so that it gets a higher average reward in the future.
These algorithms work by allowing the policy to behave randomly, observing which actions lead to high or low reward, and then positively reinforcing the actions that led to high reward, while negatively reinforcing the actions that led to low reward.
To use policy gradient methods to improve Tab, we defined a reward that encourages accepted suggestions while discouraging showing suggestions to the user that aren’t accepted. Let’s say we want the model to show a suggestion if its chance of being accepted is at least 25%. Then we could assign a reward of 0.75 for accepted suggestions, a reward of -0.25 for rejected suggestions, and a reward of 0 if no suggestion is shown. If the accept chance is p, then the expected reward if the suggestion is shown is 0.75p-0.25(1-p), which is positive exactly when p > 0.25. So a policy acting to maximize reward will suggest when it estimates the accept chance is at least 25% and show nothing otherwise.
In practice, we use a more complicated reward that accounts for the size of the suggestion as well as the possibility of jumping to other locations in the code and showing more suggestions, but this illustrates the core idea: rather than explicitly modeling the accept rate, we learn a policy that targets a particular accept rate. Presumably, the model learns in its internal representations a model of the acceptance probability (or at least a model of whether it exceeds 25%), but we leave that up to the optimizer.
The importance of on-policy data
To obtain the policy update, we rely on a remarkable fact called the Policy Gradient Theorem, which states that if a policy specifies a distribution over actions in states (i.e. the state of the user’s codebase) parameterized by , and the reward is , then the gradient of the reward is given by:
This is useful because it’s tractable to estimate the right-hand side: we can obtain samples of states and actions by sampling from the suggestions shown on user requests, we can compute using a framework like PyTorch, and we can compute by looking at whether the user accepted the suggestion. So we can use this equation to get an unbiased estimate of , allowing us to improve the policy through stochastic gradient descent.
However, this only works if the actions are sampled from the policy being optimized. Once we’ve updated the policy, we no longer have samples from the policy being optimized — we only have samples from the previous policy. To get fresh “on-policy” samples, we need to deploy the new model to users and see how it behaves. That meant we needed good infrastructure in order to quickly deploy a new checkpoint and minimize the time taken between a suggestion being shown to a user and that data making its way to the next step of our training process. Currently, it takes us 1.5 to 2 hours to roll out a checkpoint and collect the data for the next step. While this is fast relative to what is typical in the AI industry, there is still room to make it much faster.
A new Tab model
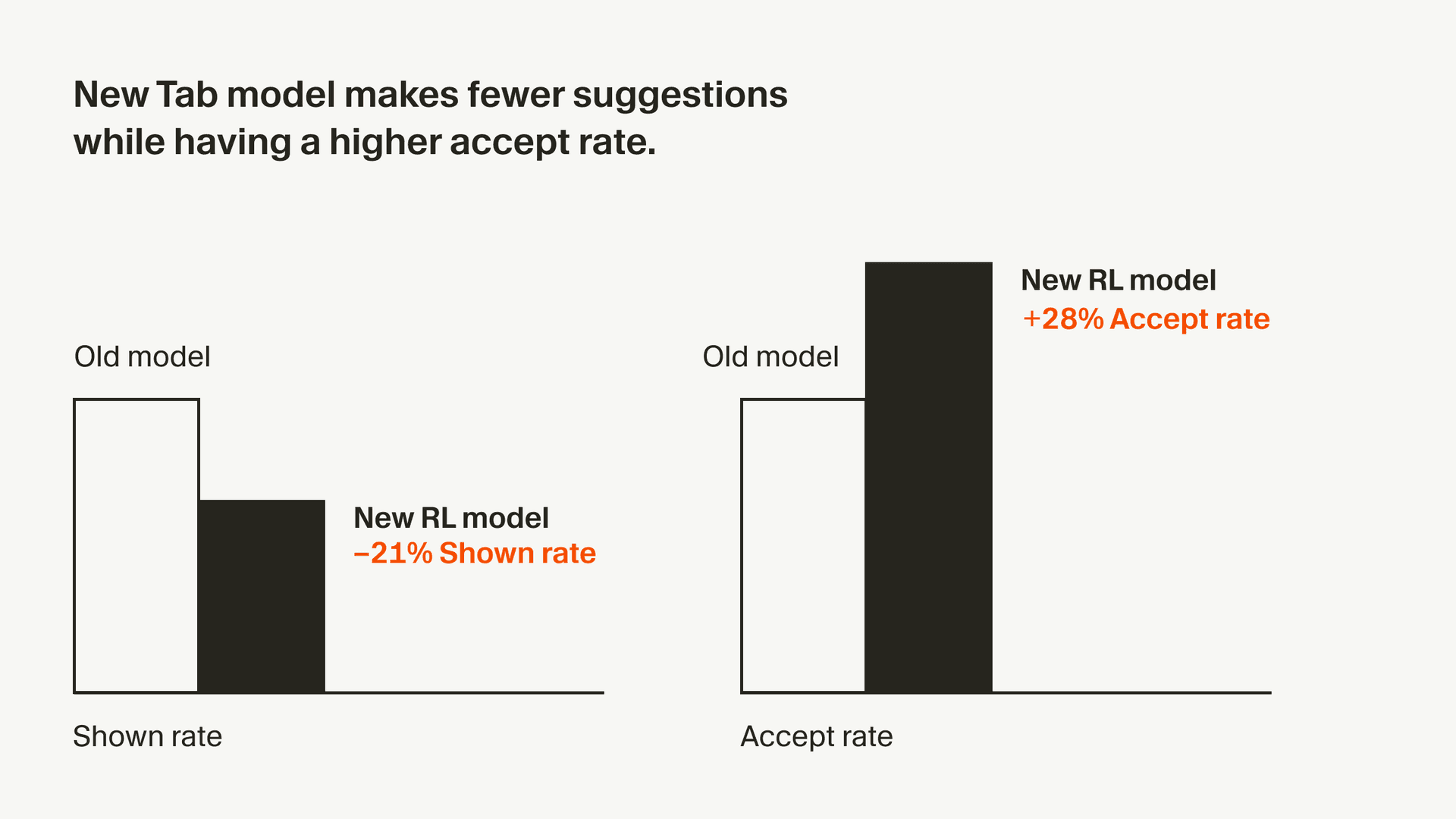
Using the methods described here, we’ve trained a new Tab model that is now the default in Cursor. This model makes 21% fewer suggestions than the previous model while having a 28% higher accept rate for the suggestions it makes. We hope this improves your coding experience and plan to develop these methods further in the future.