Inference characteristics of Llama
A primer on inference math and an examination of the surprising costs of Llama.
Llama-2-70B is an alluring alternative to GPT-3.5, but if looking for a cheap language model, it may not be worth it to deviate from OpenAI’s API.
When considering price and latency:
You should not serve Llama-2 for completion-heavy workloads
Instead, Llama is best for prompt-dominated tasks, such as classification. Llama-2 may also make sense when:
-
Your workload has no prompt tokens (unintuitive but we’ll explain later)
-
You are performing batch processing jobs
Otherwise, GPT-3.5 should be cheaper and faster.
A quick disclaimer, one reason to use Llama over GPT-3.5 is finetuning 1. But in this post, we only explore cost and latency. I don’t compare Llama-2 to GPT-4, as it is closer to a 3.5-level model. Benchmark performance also supports this claim:
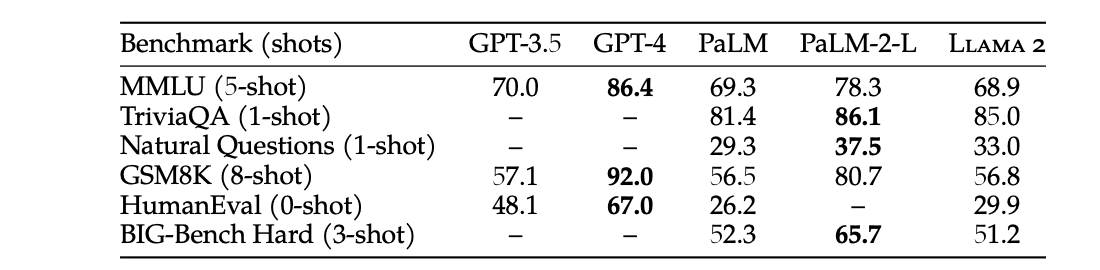
I’ll prove these assertions by comparing the cost of serving Llama-2-70B with GPT-3.5-turbo given roughly similar latencies. We serve Llama on 2 80-GB A100 GPUs, as that is the minumum required to fit Llama in memory (with 16-bit precision) 3.
On 2-A100s, we find that Llama has worse pricing than GPT-3.5 for completion tokens. We speculate competitive pricing on 8-A100s, but at the cost of unnacceptably high latency.
On the other hand, Llama is >3x cheaper than GPT-3.5 for prompt tokens.
A primer in transformer math
With some straightforward math, we will show the following for Llama-2. For a sequence length of and a batch size of :
140 comes from twice the number of parameters of the model and 320 KB/s is derived with some arithmetic. In the following section, we explain how we arrive at these numbers.
There are other papers and/or blog posts that do a fantastic job of explaining transformer math. For inference, Kipply’s post is a great reference. And, I believe Scaling Laws popularized the simplified equations used for transformer FLOPs.
To validate these numbers, we start with the architectural details for Llama. The hidden dimension is 4096, the number of attention heads is 64, the number of layers is 80, and the dimension of each attention head is 128:
Calculating model flops
The number of FLOPs for a forward pass is where is the number of parameters in the model. Every parameter in our model, belongs to some weight matrix . And for each input token, each matrix is used exactly once in a matrix multiplication with a vector representing that token.
For each , we left multiply by a vector of dimension . The total FLOPs for this vector-matrix multiplication is , or 2 times the number of entries in the weight matrix. The total number of entries in all weight matrices of the transformer is the total number of parameters, , which gives total FLOPs barring attention.
The attention contribution to FLOPs is negligible for large models like Llama with (relatively) short sequences. For each layer and each attention head, The attention operation is:
requires multiplying a vector by a matrix, which is FLOPs. The scaling factor and Softmax are negligible. Finally, multiplying the Attention vector by requires an additional FLOPs. Summing across all attention heads and layers we get MFLOPs. So for our largest sequence of 8192, attention still only occupies 10.5 GFLOPs of the full 140 GFLOPs. It’s small enough that we neglect it for simplicity.
Memory requirements are higher for completions than prompts
When generating tokens, we need to re-read all of the model’s weights and the KV-cache to generate each token. What does that mean? To perform any matrix multiplication, we need to load the weights of each matrix from RAM into the GPU's registers. With enough unique matrices, the actual loading of the weights becomes the bottleneck rather than the matrix multiplication itself. So let’s compare the path of a token through the model for prompts, and completions.
The memory path for generating tokens through a transformer
To illustrate this, we can follow the (very roughly sketched) path of a simple 1-layer transformer for generating a batch of tokens:
-
We read the input embeddings matrix, and compute the corresponding embedding vector for each input in the batch.
-
We read each of the matrices from memory to compute (vectors) for each input in the batch.
-
We perform the attention operation — which requires reading the cached keys and values. This returns a vector for each input.
-
We read from memory and multiply with the output of the previous step
-
We read the output from step 1 and add it to the output of step 4, then perform layernorm.
-
We read and multiply to get the output of the first feedforward layer.
-
We read and multiply to get the output of the second feedforward layer.
-
We read the output from step 5 and add it to the output of step 7, then perform layernorm.
-
We read the unembedding layer, then matrix-matrix multiply to get the token logprobs for each input in the batch.
-
We sample the next token and feed it back into step 1.
Let’s count up memory requirements. Across steps 1,2,4,6,7, and 9 we read all parameters of the model about once. On step 3, we read the KV cache of each batch element. On all steps, we read intermediate activations that are negligible compared to the model size. So the memory bandwidth requirements are Model Weights + KV Cache. As we increase the batch size, other than the KV cache, the memory requirements stay roughly constant! We'll come back to this later. Note that this is the memory requirement per token
The memory path for processing prompts tokens through a transformer
When processing prompts, we read all of the model’s weights once, but incur the memory cost of Attention. Consider the rough path of a batch of sequences going through the same transformer:
-
We read the input embeddings matrix, and compute the corresponding embedding matrix for each sequence in the batch.
-
We read each of the matrices from memory to compute (which are matrices)
-
We perform the attention operation
-
We read from memory and multiply with the output of the previous step
-
We read the output from step 1 and add it to the output of step 4, then perform layernorm
-
We read and multiply to get the output of the first feedforward layer
-
We read and multiply to get the output of the second feedforward layer
-
We read the output from step 5 and add it to the output of step 7, then perform layernorm
-
We read the unembedding layer, then multiply to get the token logprobs for the prompt sequences
Across steps 1, 2, 4, 6, 7 we read all parameters of the model. On step 3, we perform the attention op which, using FlashAttention, requires far less memory bandwidth than reading the model weights (for reasonable length sequences and batch sizes). On all steps, we read activations, which are matrices that are negligible compared to the model size (also for reasonable length sequences and/or batches). Note that this is the memory requirement for all tokens.
The bottomline, the memory requirement per token for prompt processing is significantly less than generating tokens, because we batch the matrix multiplication across the sequence dimension for prompts!
Memory bandwidth needed for model weights
The model weights in 16-bit precision take up GB of memory.
Memory bandwidth needed for KV cache
The size of our KV cache is the size of all keys in values for all heads for all layers in the neural net, for all of the previous tokens, which is 320 MB per token and batch element.
Llama 2 decided to remove multi-head attention. But instead of multi-query attention, they use grouped query attention, which improves performance. This results in 8 heads (or groups) for the keys and values, , rather than the normal 128 for multi-head, and 1 for multi-query.
For tokens, the size of our KV cache will be . Using 16-bit precision, that makes it KB. Given a batch size , we get KB.
For completions, this gives the memory requirement per token of:
The first term dominates for shorter sequences/small batches. Otherwise, the second term is much larger. However, since we only have 160 GB of memory and the model takes up 140 GB, the KV cache will impose a small cost on memory bandwidth in our experiments.
The memory bandwidth for prompts is around:
Communication overhead
For simplicity, we ignore communication costs as accounting for model parallelism will significantly complicate things. We can reasonably assume that it won’t add a large enough slowdown for any of our calculations (especially since we are only splitting Llama across 2 GPUs).
Prompt processing is really cheap
Prompt processing or the time to first token is the most efficient part of transformer inference, and you should expect 3x price cuts relative to GPT-3.5.
For a model with -parameters and an -length prompt, the memory requirement for processing a prompt is about Bytes, while the compute requirement is FLOPs. Since A100s can handle 312 TFLOPs of matmul and 2 TB/s of memory bandwidth, we are compute-bound for sequence lengths . 9
On A100s, FLOPs utilization will likely max out just a bit under 70% MFU. This amounts to around 200 TFLOPs. 2-80 GB A100s will cost us around $4.42/hr 10, which comes out to 0.0012/second. The FLOPs requirement for Llama is 140 TFLOPs/token. Given the aggregate FLOPs for 2 A100s, we can calculate what the tokens per second should look like:
That's a price of:
$0.00042 / 1K tokens
Compared to GPT-3.5’s $.0015 this is a steal! To be precise, it’s an almost 4x price decrease!
Latency is also quite good! On our 2 GPUs with a batch size of 1, We should be able to process 512 tokens in 170ms and 1536 tokens in 530ms.
Let’s validate these claims with actual numbers. We use an internal fork of huggingface’s text-generation-inference repo to measure cost and latency of Llama-2.
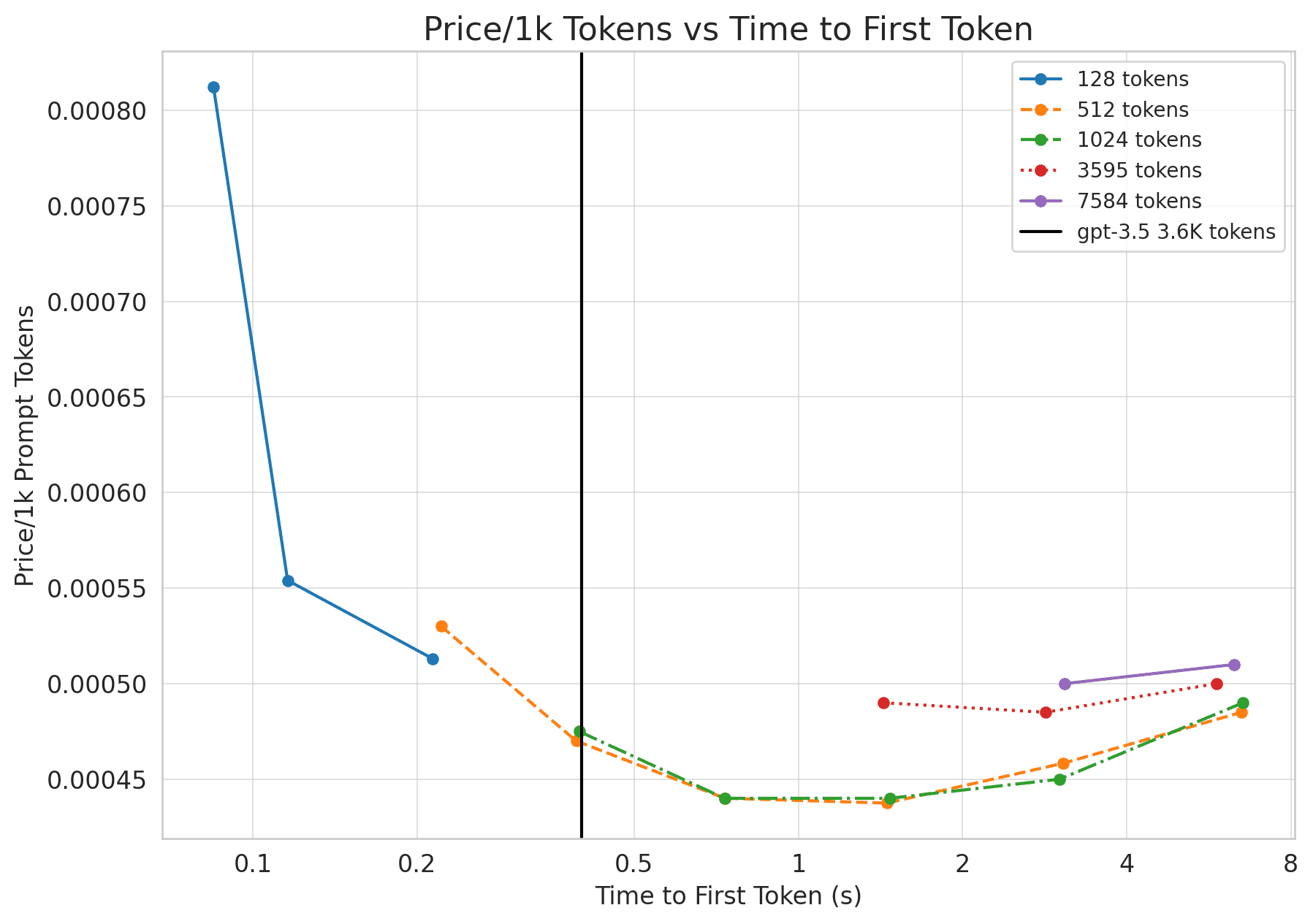
As we can see the price is significantly better than GPT-3.5’s $0.0015/1k tokens! It does look like we lag a bit behind on time to first token for longer sequences, but the solve is quite straightforward. Parallelizing Llama across 8 GPTs (instead of 2) would give us an almost 4x speedup, meaning Llama-2 dominates GPT-3.5 for prompts!
Generating tokens is slow and very expensive
In theory, it is possible to get competitive pricing to GPT-3.5 on completions, but in practice, you’ll likely do worse.
When generating tokens, we move from compute-bound to memory-bound. 11. Assuming, a batch size of 1, let’s determine the throughput we can achieve.
Each 80 GB A100 has peak memory bandwidth of 2TB/s per GPU. However, like FLOPs utilization, you can probably expect closer to 60–70% of that in inference workloads (1.3 TB/s). Since the KV cache is negligible at small batches, our throughput on 2-A100s will be:
Our new prices are much worse. At $0.0012/sec, we’re getting a cost of...
$0.066 / 1K tokens
This is abysmal pricing and speed for a GPT-3.5 level model! But remember the note from earlier on batch sizing. We’re so memory bottlenecked that we can increase the batch size with no drop in generation speed. The higher our batch size, the lower our costs.
We can’t increase to infinity, as our KV cache will eventually take up all of GPU RAM. Luckily, grouped-query attention helps alleviate this issue. For tokens, a batch size of , and 16-bit precision, our cache will be Bytes. In the case of 4096 tokens, this equates to 1.3 GB of memory for a batch size of 1. We have 160 GB of space on our 2-A100 machine. Our model takes up 135 GB of this, leaving just 25 GB of space for the KV cache. Due to additional inefficiencies in memory storage. our max batch size for longer sequence lengths is around 8.
Given the (roughly) 8x speedup, we can expect a price of $0.00825 / 1K tokens. This is still worse than GPT-3.5-turbo, but closer. For shorter sequence lengths (1k total tokens), we should be able to increase the batch size to 32, meaning a price of $0.00206 / 1K tokens. In theory, this is competitive with GPT-3.5-turbo.
Another solution is increasing the number of GPUs. By renting 8-80 GB A100s, we get 1.28TB of memory. Removing the model weights, we have over 1TB of memory left over for the KV cache, meaning a batch size of >512 tokens is possible. Note that we won’t actually see a 512x cost decrease, as the KV cache now takes up 8x more memory bandwidth than the model size, meaning it would be closer to a 64x cost decrease.
Using more compute also solves the latency issue. GPT-3.5 hits around 70 TPS. Splitting the model across 8GPUs instead of 2 should bring us around 74.4 tokens/s.
We didn’t have access to 8 A100s when running this experiment, but let’s take a look at the numbers on 2-80 GB A100s:
Measured generation performance
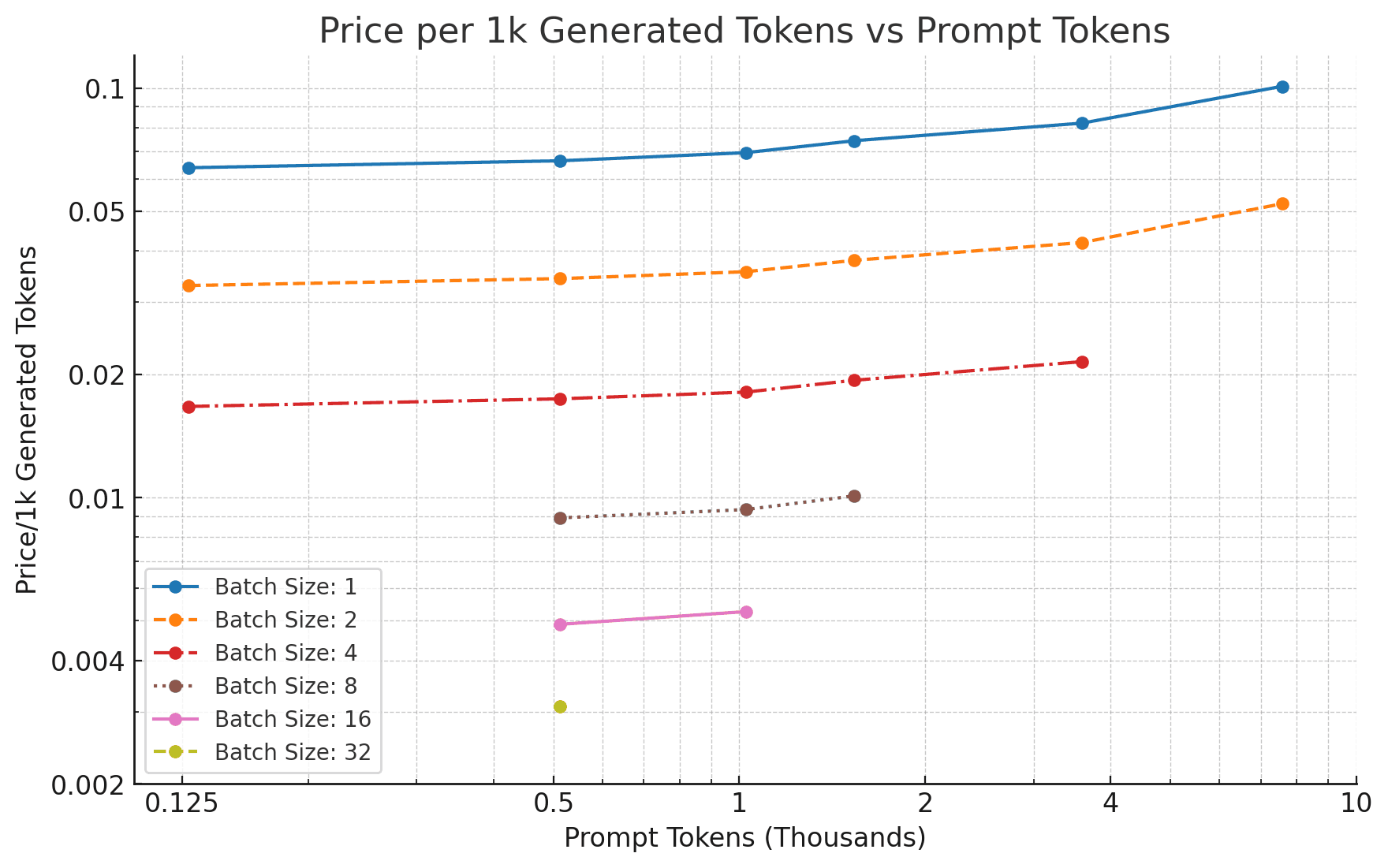
These numbers are pretty close to what one would expect given the memory bandwidth calculations.
As we can see, increasing the batch size directly results in almost linearly decreasing costs for price/1K tokens. However, we still trail a decent bit short of GPT-3.5 pricing of $0.002/1K tokens — especially for longer sequence lengths.
Large Batch Sizes Mean Unacceptable Latency
Running generation with large batch sizes means GPT-3.5 competitive pricing, but it spikes the time to first token. As we increase our batch size, costs go down linearly, but time-to-first token also increases linearly.
A batch size of 64 brings us to better pricing than GPT-4. But, a batch size of 64 gives us:
-
A time to first token of almost 3 seconds for only 512 tokens!
-
A batch size of 64 for 3596 tokens is 20.1 seconds.
As a result, the kinds of workloads where Llama-2 would make sense relative to OpenAI’s API are:
-
A large prompt with little to no generated tokens — handling pure prompts is remarkably simple.
-
Generating tokens with a small or no prompt — we can tune the batch size up to >64 and get competitive pricing with GPT-3.5-turbo without sacrificing latency.
-
Offline batch-processing jobs that are not latency-critical.
Turning up the batch size requires consistently large workloads, which most startups will not have! For most users and most workloads, usage is incredibly bursty. Of course, a candidate solution is auto-scaling up and down on-demand GPUs, but even so, you can probably expect on average 50% of max throughput per-GPU — especially given cold boot times.
Our recommendation is to use open-source models for prompt-heavy tasks and leave generation-heavy tasks to closed-source models like GPT-3.5
Quantization
Most quantization methods are lossy, meaning some performance degredation. We can likely achieve mostly competitive performance with 8-bit quantization, giving a 2x price decrease on all calculated numbers! Quantization and imperfect utilization cancel each other out, meaning accounting for both, we expect similar prices to what we’e measured!
However, the goal of most open-source quantization methods is to allow easy deployment on few/small consumer GPUs rather than optimized throughput at scale.
There are several open-source libraries that optimize for even lower precision quantization while maintaining performance. However, these libraries optimize for serving these models on few/small non-datacenter GPUs rather than throghput at scale. Specifically, they optimize for the low-batch inference case (mainly a batch size of 1). Despite offering (at best) 3–4x speedups, that still corresponds to a price of $0.017/1K tokens.
Bits and Bytes
Bits and Bytes offers (effectively) lossless quantization, meaning no difference in performance. However, it’s main benefit is reduced memory usage rather than speed. For example the speedup of the recent NF4 representation is only on matmul speed, rather than inference throughput. Empirically, people don't seem to be measuring speedups on that front.
It is also unclear how well it scales to larger batches.
Llama.cpp
I believe Llama.cpp is mainly optimized for Apple hardware. They also have Cuda support, and support fast 4-bit precision for inference, but my suspicion is naive quantization here would result in significantly degraded performance.
Also, this library is optimized for the low-batch regime.
GPT-Q
GPT-Q is another quantization library. I have not tested GPT-Q, but plan on doing so. Hopefully we can see a 2x price reduction here!
Once more, the implementation is optimized for the low-batch regime. In addition, the >3x speedup reported in the paper is only for 3-bit quantization, which is too lossy our use-cases.
How exactly are closed source models cheaper?
There are several methods closed-source models use to be dramatically speed up inference
Quantization
As mentioned earlier, there are several solid open-source quantization methods - but I suspect OpenAI’s quantization implementations are better optimized for larger batches.
Mixture of Experts
it is widely speculated GPT-4 uses mixture of experts 15. If GPT-3.5-turbo also uses MOE, then for the same level of performance you can serve a MUCH smaller (and therefore faster) model
Speculative sampling
Speculative sampling is another interesting trick that gets around the slow decoding time of language models by having a smaller model draft several tokens in a row. 16. Note that in the limit this will not offer significant increases in throughput, but can drastically reduce latency. For reference, this repo implements a simplified version of it.
Fancy tricks for inference at scale
When running inference at scale, OpenAI can probably do fancy things like allocate several 8-GPU nodes for prefilling a batch of requests, then allocate a single 8-GPU node for generating tokens on that batch of requests. This would give them the best of both worlds, where they can use batch sizes > 64, and still see a ridiculously low time to first token.
Closing thoughts
We’ve used these findings to inform how/when we decide to use Open-source models at Cursor.
To recap, we find it most helpful to use open-source models for prompt-heavy tasks, such as classification or reranking
Come work with us at Cursor!
We’re building Cursor, an AI-first code editor. When fundamentally re-imagining the development environment, we get to tackle loads of very interesting problems. For example, finetuning and serving models for a fraction of the price of OpenAI’s API. Or designing new abstractions for creating complex chains and agents with OpenAI’s API.
We’re a small team of 9 based out of SF and backed by OpenAI. If interested, please reach out at hiring@cursor.com.
Or, if you want to talk shop about language models, DM me on Twitter.
Appendix
Below is the table of datapoints with measurements on Llama-2-70B latency as well as some additional calculated metrics
| Batch size | Prompt tokens | Completion tokens | Time to first token | Time for completion | Tokens/s | Prompt TFLOPs/GPU | Prompt memory bandwidth/GPU | Prompt FLOPS Util | Prompt Memory Util | Price/1k prompt tokens | Price/1k Completion tokens |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 128 | 242 | 0.084 | 12.636 | 19.151 | 106.156 | 1.341 | 0.340 | 0.894 | $0.00081 | $0.06412 |
| 2 | 128 | 512 | 0.116 | 27.751 | 18.450 | 154.478 | 1.291 | 0.495 | 0.861 | $0.00056 | $0.03328 |
| 4 | 128 | 512 | 0.216 | 28.154 | 18.186 | 165.706 | 1.273 | 0.531 | 0.849 | $0.00052 | $0.01688 |
| 1 | 128 | 242 | 0.084 | 12.661 | 19.114 | 106.122 | 1.338 | 0.340 | 0.892 | $0.00081 | $0.06425 |
| 2 | 128 | 512 | 0.116 | 27.824 | 18.402 | 154.196 | 1.288 | 0.494 | 0.859 | $0.00056 | $0.03337 |
| 4 | 128 | 512 | 0.215 | 28.205 | 18.153 | 167.074 | 1.271 | 0.535 | 0.847 | $0.00051 | $0.01691 |
| 1 | 512 | 512 | 0.217 | 27.752 | 18.449 | 164.996 | 1.291 | 0.529 | 0.861 | $0.00052 | $0.06656 |
| 2 | 512 | 512 | 0.392 | 28.543 | 17.938 | 183.068 | 1.256 | 0.587 | 0.837 | $0.00047 | $0.03423 |
| 4 | 512 | 512 | 0.734 | 29.042 | 17.630 | 195.345 | 1.234 | 0.626 | 0.823 | $0.00044 | $0.01741 |
| 1 | 512 | 304 | 0.225 | 16.393 | 18.545 | 158.940 | 1.298 | 0.509 | 0.865 | $0.00054 | $0.06622 |
| 8 | 512 | 512 | 1.445 | 29.753 | 17.208 | 198.402 | 1.205 | 0.636 | 0.803 | $0.00043 | $0.00892 |
| 8 | 512 | 512 | 1.460 | 29.740 | 17.216 | 196.344 | 1.205 | 0.629 | 0.803 | $0.00044 | $0.00892 |
| 16 | 512 | 512 | 3.081 | 32.708 | 15.654 | 186.149 | 1.096 | 0.597 | 0.731 | $0.00046 | $0.00490 |
| 16 | 512 | 512 | 3.038 | 32.661 | 15.676 | 188.776 | 1.097 | 0.605 | 0.732 | $0.00046 | $0.00490 |
| 16 | 512 | 512 | 3.068 | 32.708 | 15.654 | 186.887 | 1.096 | 0.599 | 0.730 | $0.00046 | $0.00490 |
| 32 | 512 | 512 | 6.363 | 41.302 | 12.396 | 180.256 | 0.868 | 0.578 | 0.578 | $0.00048 | $0.00310 |
| 32 | 512 | 512 | 6.632 | 41.099 | 12.458 | 172.931 | 0.872 | 0.554 | 0.581 | $0.00050 | $0.00308 |
| 1 | 1024 | 512 | 0.397 | 28.961 | 17.679 | 180.727 | 1.238 | 0.579 | 0.825 | $0.00048 | $0.06946 |
| 1 | 1024 | 512 | 0.396 | 28.982 | 17.666 | 181.017 | 1.237 | 0.580 | 0.824 | $0.00047 | $0.06951 |
| 2 | 1024 | 512 | 0.732 | 29.674 | 17.254 | 195.759 | 1.208 | 0.627 | 0.805 | $0.00044 | $0.03559 |
| 4 | 1024 | 512 | 1.471 | 30.159 | 16.977 | 194.904 | 1.188 | 0.625 | 0.792 | $0.00044 | $0.01808 |
| 8 | 1024 | 512 | 3015 | 31.167 | 16.428 | 190.223 | 1.150 | 0.610 | 0.767 | $0.00045 | $0.00934 |
| 16 | 1024 | 512 | 6.541 | 35.111 | 14.582 | 175.325 | 1.021 | 0.562 | 0.681 | $0.00049 | $0.00526 |
| 1 | 3595 | 512 | 1.430 | 34.210 | 14.966 | 175.929 | 1.048 | 0.564 | 0.698 | $0.00049 | $0.08205 |
| 2 | 3595 | 512 | 2.841 | 34.964 | 14.644 | 177.168 | 1.025 | 0.568 | 0.683 | $0.00049 | $0.04193 |
| 4 | 3595 | 512 | 5.846 | 35.795 | 14.304 | 172.199 | 1.001 | 0.552 | 0.667 | $0.00050 | $0.02146 |
| 1 | 7584 | 166 | 3.081 | 13.641 | 12.170 | 172.330 | 0.852 | 0.552 | 0.568 | $0.00050 | $0.10091 |
| 2 | 7584 | 512 | 6.296 | 43.482 | 11.775 | 168.642 | 0.824 | 0.541 | 0.550 | $0.00051 | $0.05214 |